スクラッチに挑戦している皆さん、どうも!スクラッチコーチです。
- ① まずはパソコン操作の部分を作る
- ② マルチタップのモバイル対応スティックを完成させる
- ③ アクションゲームをモバイル対応してみる
- ④ 自由回転するスプライトの向き(角度)をスティックで算出する (いまここ)
- ⑤ スイカゲームをモバイル対応してみる
スーパーアルティメットにマニアックなチュートリアルへようこそw
こんなチュートリアル読む人おる?という気持ちもあるけど、一応書いておこうかなって思ってる。もしここにたどり着いた人がいるなら、ウェルカム、君のために書いたと言っても過言ではないぜ。
で、結論から言うとatanという関数を使うと便利。
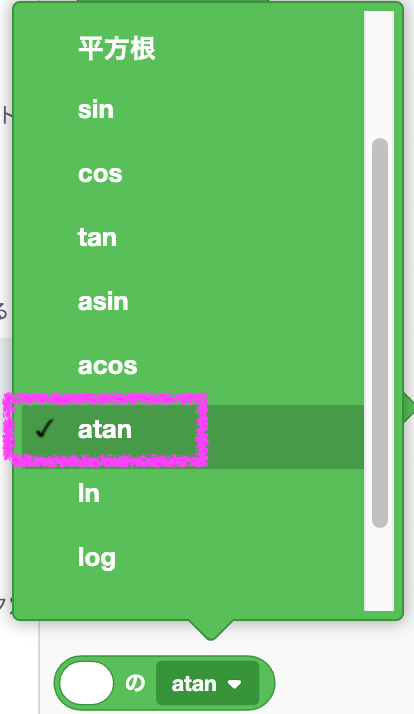
これね。アークタンジェントって中二病キャラの必殺技みたいな名前で草。

高校1年か2年で習うらしい。僕は数学やらなくていい高校だったから知らないw
三角関数のsinとcosは習った記憶あるけど、当時は興味ゼロだったw tanに関しては当時の数学の先生が「君らは(英語学科だから)覚えんでもええよ」ってwだからマジでatanとか習ってない……。
ちなみにPythonとかだともっと便利なatan2という関数があって、XとYから角度を求めるのがカンタンなんだけど、スクラッチにはatan2はないのでatanを使って強引に角度を算出する方法を紹介していくぜ。
でも前述したように僕は数学あんまだから、この方法がベストではないかも知れない。でも出来たから紹介する!プログラミング業界では「動くのは正義」という考え方があって、方法論が違ってても正しく動くならとりあえずOKというのは決して悪くないスタンスなのだ!
今回ももちろんモバイル対応スティックを使っていくよ。

モバイル対応のチュートリアルはもう見たかな?もし自分のプロジェクトにスティックがないという人は、チュートリアルで一緒に作るか、こちらのプロジェクトからスティックをバックパックしよう。
今回の目的「スティックに合わせて、自由回転するプレイヤーの向きを変える」
回転が左右だけなら、スティックXがプラスかマイナスかで向きを変えればいいだけなんだけど、自由回転する場合はいっきに複雑になる。そこをatanを使って強引に算出していく。
まずは実現する動きを動画でチェックしてみてね↓
これを作るよ。今回はこの動きだけ作るからブロック数は少なめ!
メインループを作る
じゃあ緑の旗から始めようか。

スクラッチキャットの回転方法を「自由に回転」にしておこう。

メインループを設置しよう。
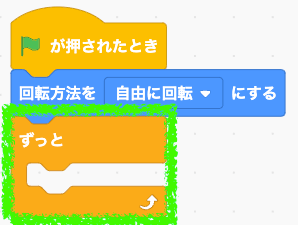
この中で向きの計算をしていくよ。
準備
スティックの場所に合わせて向きを算出する処理、今回の目的部分だね!
バックパックからスティックを導入して、あとは分かりやすくブロック定義と変数も作るよ。そうすれば別の作品にも使いやすいだろうし。
スティックを導入する
バックパックからスティックをドラッグアンドドロップしよう。
スティックを開く必要はないよ。スクラッチキャットを開いておいてね。
ブロック定義を作る
スクラッチキャットにブロック定義「_向きを算出する」を作ろう。再描画せずに実行するよ。パッと見で分かるように接頭語にアンダーバーを付けておくね。
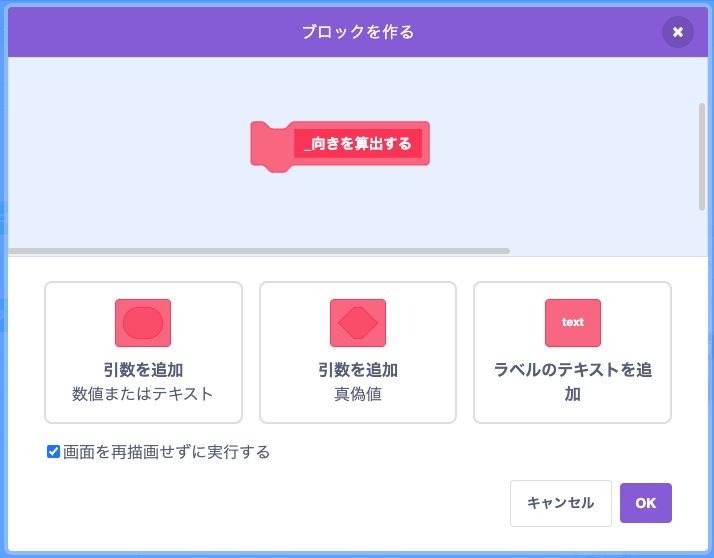

接頭語で変数やブロック定義などの種類をパッと見で分かるようにする方法は、コーディング規約としてまとめてあるよ。興味がある人はチェックしてね。
変数を作る
変数「向き」を作るよ。
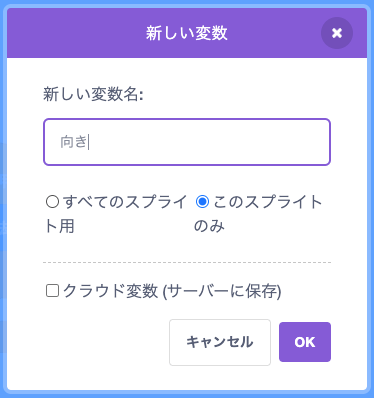
atanを使ってみる
では練習でアークタンジェントを使ってみよう。一般的にはatan(Y / X)のように、atanにはY÷Xを与えるっぽい。
Xがプラスのとき
いくつかサンプルを見ながらatanがどういう解をくれるのかチェックしていこうか。
右上を向きたい
仮にYが1でXも1の場合を考えてみよう。
スティックの位置が↓こんなかんじになってる状態ね。
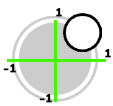
スティックが右上にあるときは、スプライトも右上を向いてくれたらバッチリだよね。
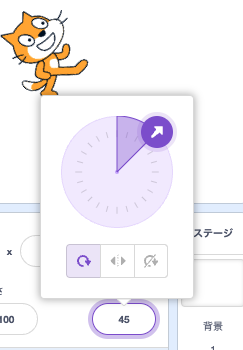
じゃあatanでYが1でXが1の状態を作ってみよう!

おお!見事に45っていう数値が出てきたね。
右を向きたい
では真横に動くようなケースではどうだろうか。
Yが0で、Xが1のときだね。
スティックは↓こんな感じ。

スプライトの向きは90になってほしい。
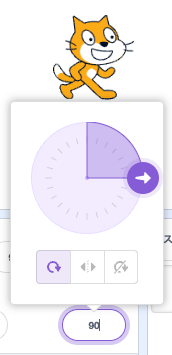
atanに入れてみよう。

あれ?違うね……。うまくいかない。
右下を向きたい
次はYが-1で、Xが1のときはどうかな。
スティックは↓こんな状態だね。

スプライトの向きは135になってほしい。
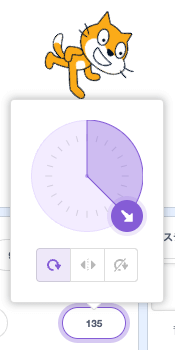
atanで作ってみると……。

あらら、これも違うみたいだね。
上を向きたい
Y = 1、X = 0。だからスティックは↓こう。

ほしいのは↓みたいに0°。
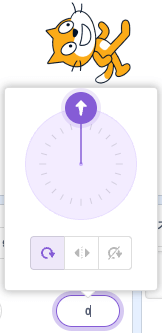
atanの解は……。

90°になってしまった……いったいどうなってるんだ!?
ズレに法則性がある
ズレてる、atan使えねぇ……そう諦める前にズレ方に注目してほしい。
| ほしい角度 | atanの解 | |
| 右上:◯ | 45 | 45 |
| 右:✗ | 90 | 0 |
| 右下:✗ | 135 | -45 |
| 上:✗ | 0 | 90 |
なーんか法則性がある気がする。ためしに色々な数字を掛け合わせてみたところ「90 - atanの解」をするとズバッと欲しい角度が取れた。
| ほしい角度 | atanの解 | 90 - antaの解 | |
| 右上:◯ | 45 | 45 | 90 - 45 = 45 |
| 右:◯ | 90 | 0 | 90 - 0 = 90 |
| 右下:◯ | 135 | -45 | 90 - (-45) = 135 |
| 上:◯ | 0 | 90 | 90 - 90 = 0 |
くっ、よく考えたら当たり前だったんだけど、一応図解しておくぜ!
合ってたケース(右上)
たまたま合っててぬか喜びした。
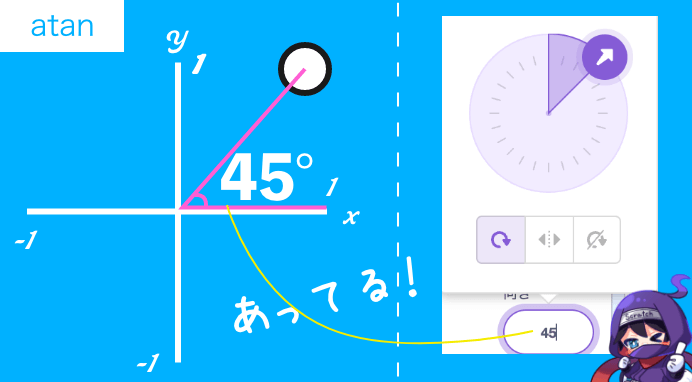
計算結果が合わないケース(上)
右上以外ダメじゃん、って気づいた。
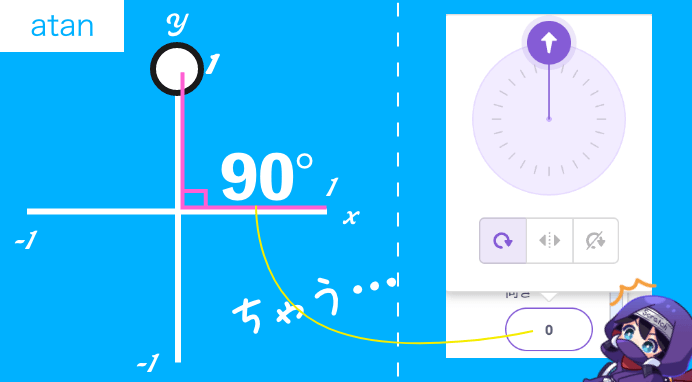
よく考えたらそもそも90°ズレてた
試行錯誤して0°のケースを自分なりに図にしてみたら、そもそもatanが算出してくれる角度って、スクラッチの向きと90°ズレてるじゃんって気づきました、本当にありがとうございました。
↓のピンクの先の部分。90°ズレてるよね、うん。
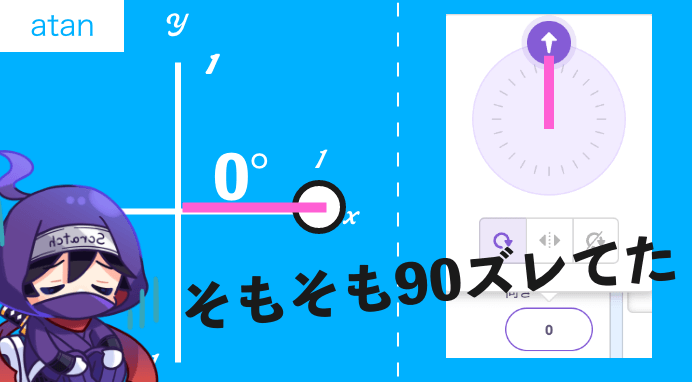
だから90からatanの値をマイナスすると上手いこと計算が合ってたというカラクリでした。

数学オンチ……この解答ももっとスマートなやり方があるのかもしれない……あるならぜひリミックスして教えていただきたいです。
Xがマイナスのとき
さらに数学オンチな僕を混乱させてくれたのは、Xがマイナスのときな!
左上を向きたい
たとえばY = 1でX = -1のとき。

ほしい角度は-45°。
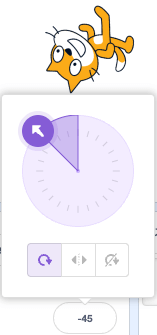
atanの解は……。

合ってるんかい!でも90からマイナスすることにしたから、90 - (-45) = 135になってしまう!く……。

まぁここは焦らず条件ブロックを使いましょうぜ。Xがマイナスのときは、90からマイナスしなければいいではありませぬか?

うむ、そうだな。しかし、念のため左とかもatanしてみようぞ。
左を向きたい
Y = 0、X = -1のときだね。

ほしい角度は-90°!
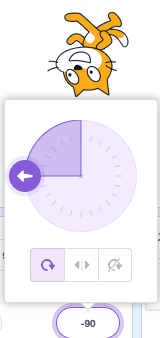
atanの解は……。

ゼロぉ!!!なんだそれぇ!!!
atanは負の象限を返してくれない
調べたよ、ウィキペディアで。そしたらatanは負の象限は返さないって感じのことが書いてあった。

負の象限とは、ここではつまりXがマイナスの時って解釈でOK。
よく分からないから更にググったら、atanで無理やり負の象限を出したいときは180°マイナスしたらいいと書いてあった。
いや、atanの解は0でほしいのは-90だから、シンプルに-180したらダメじゃん……っと思って気づいた。

せや、スクラッチの向きは90°ズレとるんやった……
そこでXがプラスのときと同じようにいったん90 - atanの解をしてから、更にマイナス180してみたところ。

取れたぁ!!-90獲ったどぉ!!
久しぶりに数学的なモヤモヤで脳みそが千切れそうになったぜ……やるな、スクラッチ!
コーディングしていく
よし、atanの基本的な解答とスクラッチのクセを組み合わせるロジックは見えた。あとはコーディングしていくだけだ!イケる気がする!
基本的なatan演算
まずは基本形を作ろう。

YをXで割るという順番だけ注意しよう。
90から引く
スクラッチの向きは上が0°であるのに対して、atanでは右が0°という想定なので、このズレを補正するべく90からatanの解答を引くようにする。

向きにセットする
変数「向き」にセットしよう!

Xがマイナスのときに反転させる
さらにatanでは負の象限を返してくれないので、Xがマイナスなら強引にマイナス180°しよう。
条件分岐をおいて……

スティックXがマイナスなら……

マイナス180しよう!

向きを割り当てて完成!
ではメインループに戻って、このブロック定義を呼び出して向きを変えてみよう。

変数「向き」を向きに割り当てる……書くと意味不明w

動けぇ!
OK!
分かりづらい解説によく付いてきてくれた!ありがとう!これでグリグリ回る仕組みが整ったね!
実はスプラトゥーンをモバイル対応してみようとしてた
そう、この回転をやろうと思ったきっかけはFunnyAnimatorJimTVさんのスプラトゥーンをリミックスしたいなっていう動機だったんだよ。
グリグリ回るし、歩くのもできたんだけど、iPadでテストしようとしたらスプラトゥーンのプロジェクトが大きすぎてiPadでロードできなかったw
モバイル対応しても意味ないじゃんって気づいて、せっかくだからこの自由回転のロジックだけでも世に出してあげたいと思って書き上げた記事でした!読んでくれてありがとう♪
- ① まずはパソコン操作の部分を作る
- ② マルチタップのモバイル対応スティックを完成させる
- ③ アクションゲームをモバイル対応してみる
- ④ 自由回転するスプライトの向き(角度)をスティックで算出する (いまここ)
- ⑤ スイカゲームをモバイル対応してみる

アスクラッチで質問する
スクラッチャーからのコメント

























































