Scratchペン道部③　星型に挑戦する

スクラッチに挑戦している皆さん、どうも！スクラッチコーチです。

スクラッチのペン道部へようこそ！モチモチスライムで有名なnakakoTVさんのペン講座とコラボしたScratchペン道部の練習場だぞ。

今回のゴール

まずは四角形のリファクタリングを行ってから、複雑な図形の描画に挑戦していく。ペン道は長く険しい。迷子にならないように一歩一歩すすもう！

四角形のリファクタリング

前回作った四角形だけど、もっともっと数学的に工夫すればカンタンで洗練されたプログラミングに作り変えられる。

微調整

基点XとYの初期値にカメラを反映させたほうがわかりやすい！

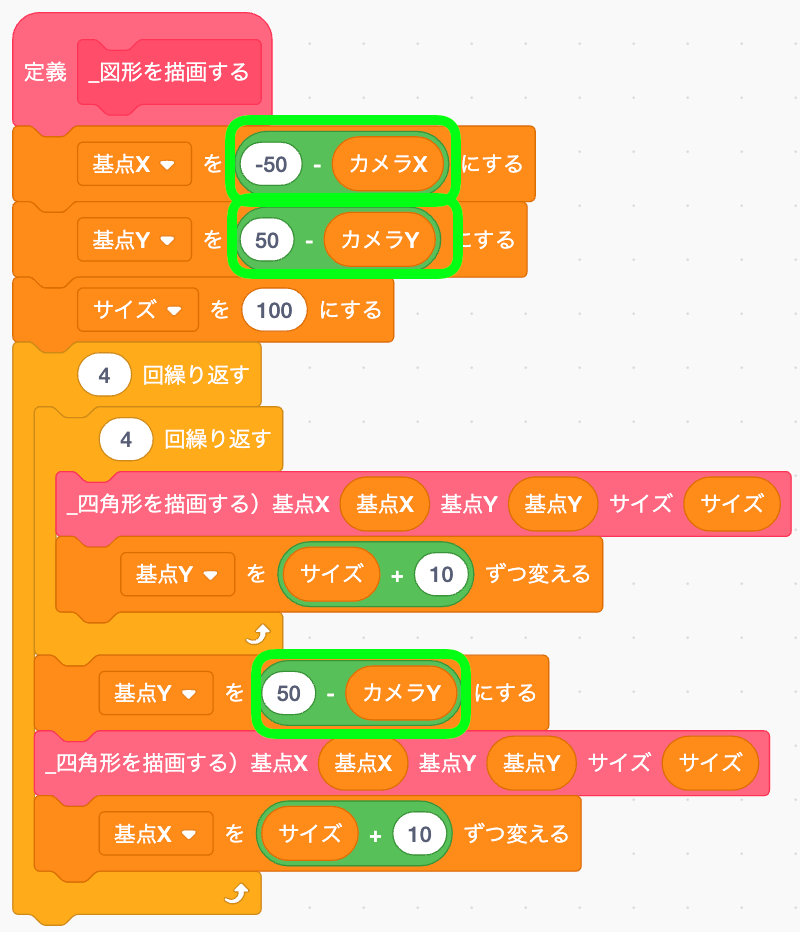
ペンの色は図形を描く直前で指定できるようにしておく。

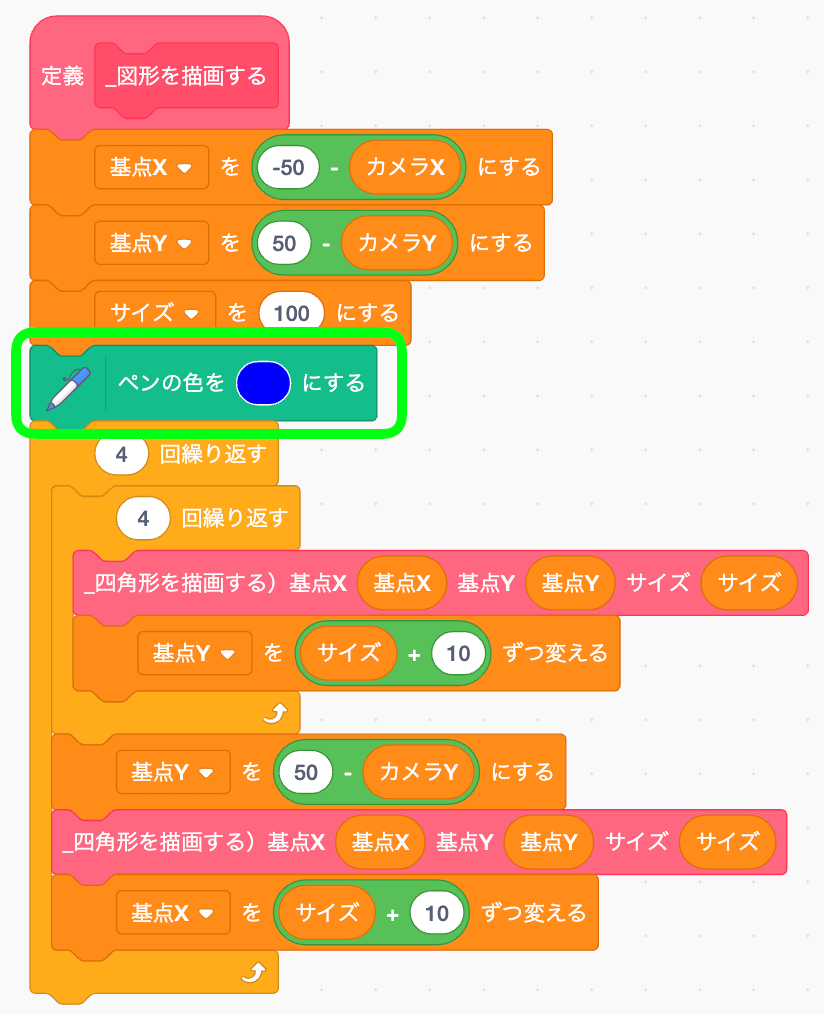
向きを変えればカンタンに描ける

今はA地点からB地点まで線を描く、みたいな作戦だったよね。これはシンプルだから最初の理解としては役立つ。でも回りくどい描き方でもあるんだ。

そこで、四角形の書き方をガラリと変えてしまいたい。

まずはここで切り離しちゃおう。まるっと。

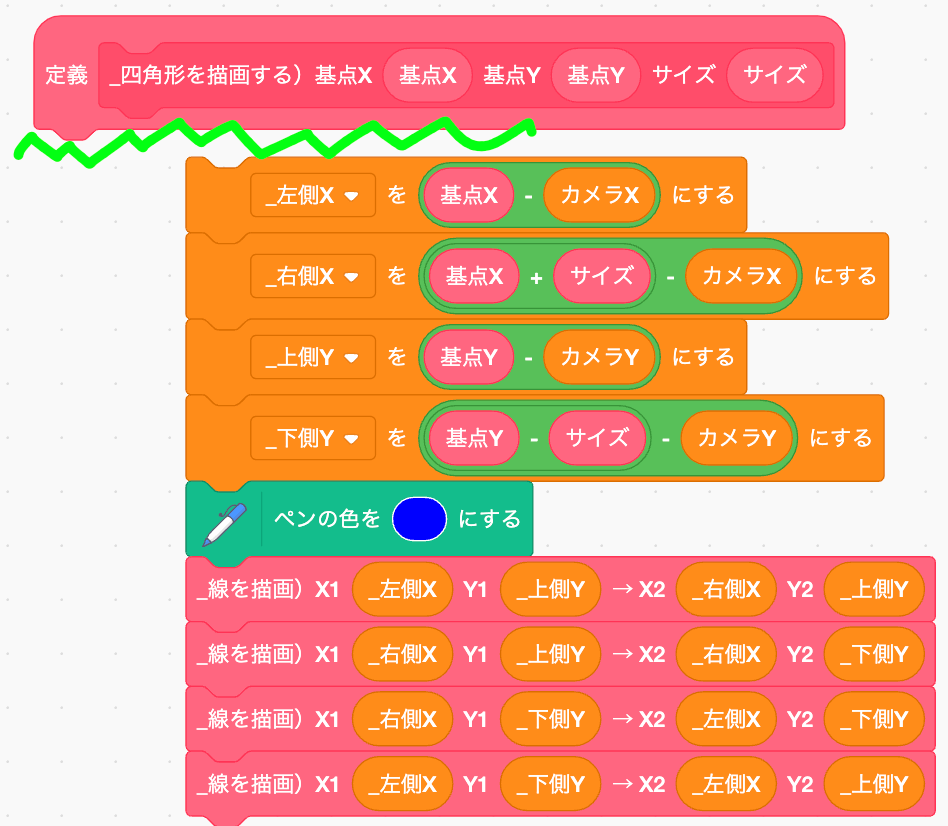
そしたらシンプルに線を描く実装を行う。いつもと違うのは、ペンの上げ下げの順番。いつもは、ペンを下ろして→動かして→ペンを上げる、という順番だけど、ここでは逆。下ろしたままの状態にしてほしい。

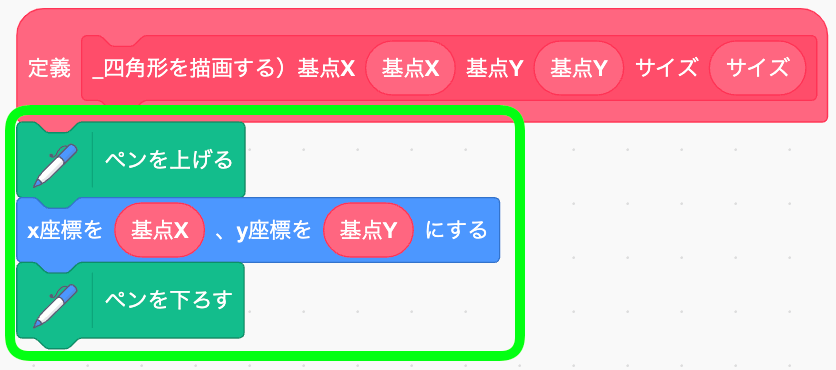
ペンを下ろしたまま、スクショのように繰り返し処理を作ろう。

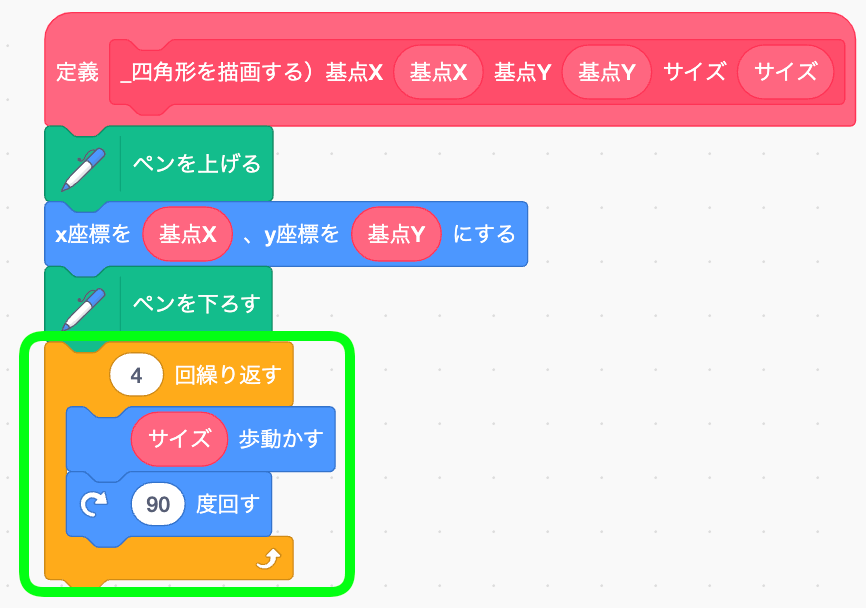
どうなってるの？

これで何をしてるかというと、まず繰り返しの前にペンを下ろしてあったよね。

・

この段階ではまだ線を引いたわけではなくて、チョンって点を描いただけ。「・」とだけ描かれてる状態だね。

━

で、そこから1回サイズの大きさだけ「○歩動かす」と1本の横線が引ける。「━」って状態。

┓

そして90度右に回す。そうすると下を向いてることになる。ここから2回目の「○歩動かす」を実行すると下に向かって線が描ける。「┓」って状態。

コ

再び90度右に回り、左を向かせる。3回目の線を引いて「コ」の状態になる。

□

ラストもう1回90度右に回して上を向き、4回目の線を引けば「□」の状態が完成するという寸法だ。

変わりないかテストする

よしよし、リファクタリングは「より洗練されたコーディングで同じ動きを実現する」ことが目的だから、何も変わってないことは良いことなんだ。

移動可能な距離を無限大にする

さて、今のままでも矢印キーでカメラを動かせば図形は画面外に消えるよね。

でもこれには限界があって、ある程度押し続けると座標は止まってしまうんだ。

これ以上は動かない。大きな図形を描いたり、広い場所を作りたくなったら困ることもある。

そこで、コスチュームの無限化というテクニックを使っておこうと思う！

コスチュームを描く

新しくコスチュームを描こう。

初期状態だと何も描かれてないはずなのにサイズが2x2になっている。ないはずなのに、ある。ホラーだね、、、（笑）

サイズのゼロ化

サイズゼロのコスチュームを作る方法は簡単。適当な図を描くために四角形ツールを選ぼう。

なんでもいいので描いてみて。

選択ツールに持ち替えよう。

さっき描いた図を選び、削除する。

たららーん！サイズゼロのコスチュームができたぞ。

コスチュームの名前は「無」とかにしようか。

変な割り算をする

コスチュームを無に着替えて、大きさを「1 / 空白」%にしてみよう！これが無限大コスチュームを作る秘密の割り算だ。

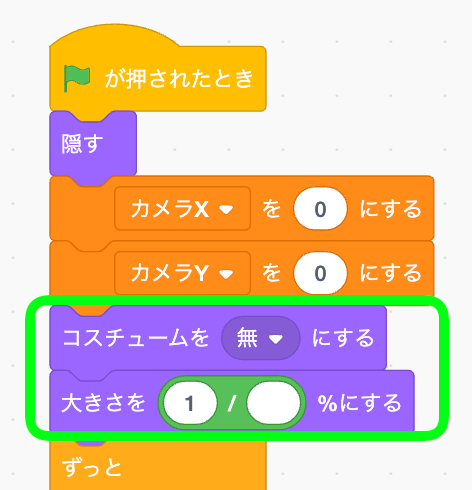
これでキーを押し続けてみると、、、

わぉ！どこまででも動けるようになったぜ！！自由だ…！

キー入力をリファクタリングする

次に、キー入力も洗練しようかな。がっつり消そう。、

代わりに変な引き算を作る。

• カメラXには「右向き矢印キーが押された ー 左向き矢印キーが押された」に10をかける
• カメラYには「上向き矢印キーが押された ー 下向き矢印キーが押された」に10をかける

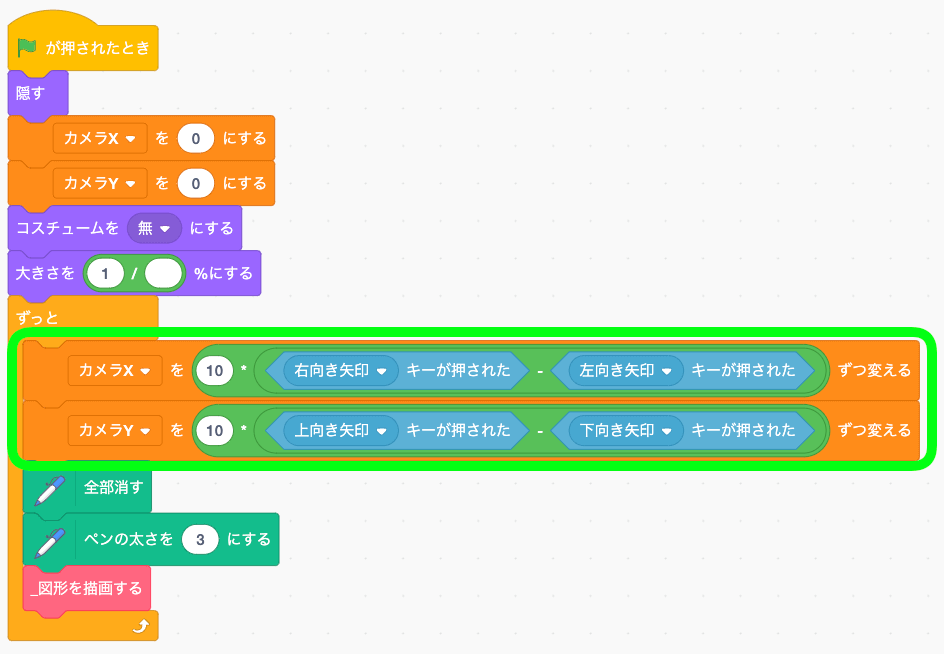
これで元々あった縦長のブロックと同じ動きになる。グリフパッチさんもよく使うテクニックだよ。

キーが押されたら1になる

何が起きてるかというと、「右向き矢印キーが押された」ブロックの、次の特徴を利用しているんだ。

• キーが押されたら1になる
• キーが押されてないとゼロになる

つまり「右向き矢印キーが押された　ー　左向き矢印キーが押された」という式は次のようになる。

• 右が押されたなら「1 - 0」= 1。10かけて10になる。
• 左が押されたなら「0 - 1」= -1。10かけて-10になる。
• 何も押されてなければ「0 - 0」= 0。10かけてもゼロ。

数学的なトリックとしてはシンプルだね。でも強力だから、どんな作品にも使いやすい。

複雑な図形「星形」に挑戦する

さて、ここまではシンプルな四角形や三角形を描いていた。ここらで複雑な形に挑戦しよう。

丸にする？

いやいや、、、。

丸くなるな、星になれ！（CM（笑））

ということで星形に挑むぞ。星を描くのにさっき学んだ四角形の描き方が役立つ。そう、四角形のリファクタリングは星を描くための壮大な前振りだったのであるw

まずは四角形をたくさん描いてる部分は外してしまおう。

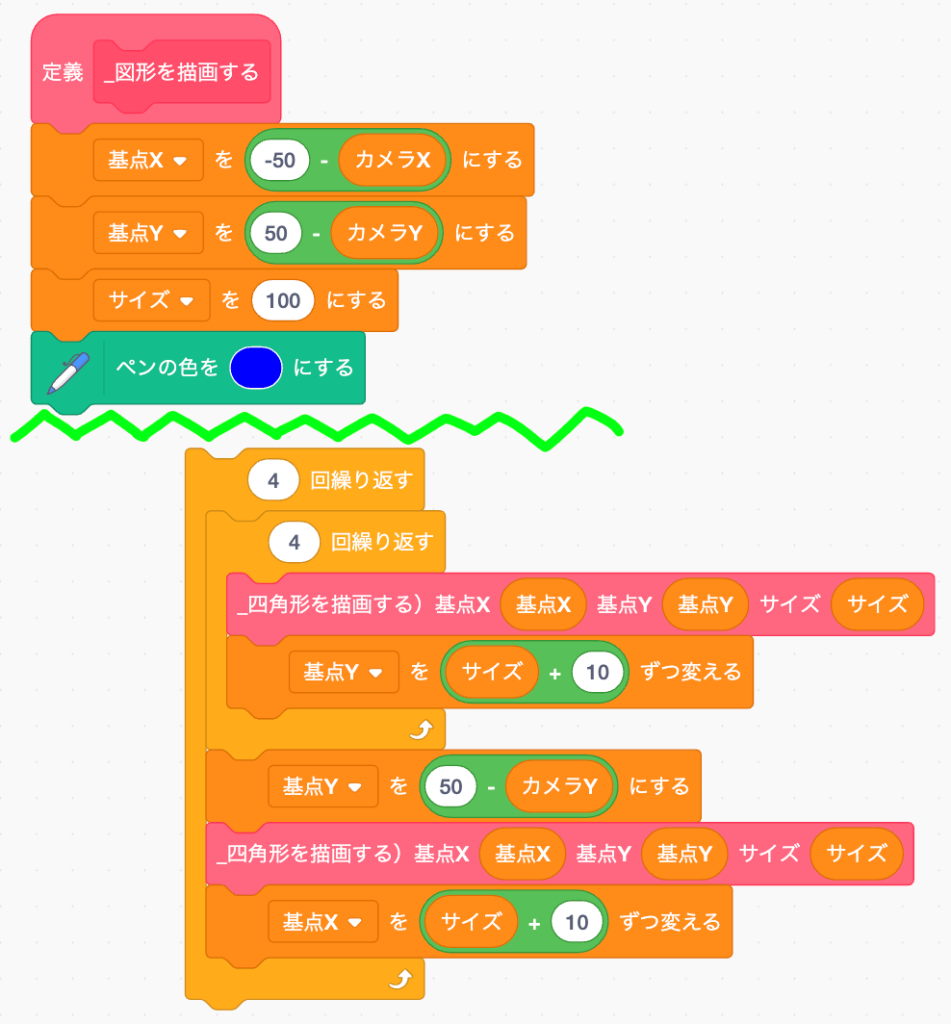
定義「_星形を描画する」を作る

新しく定義を作る。

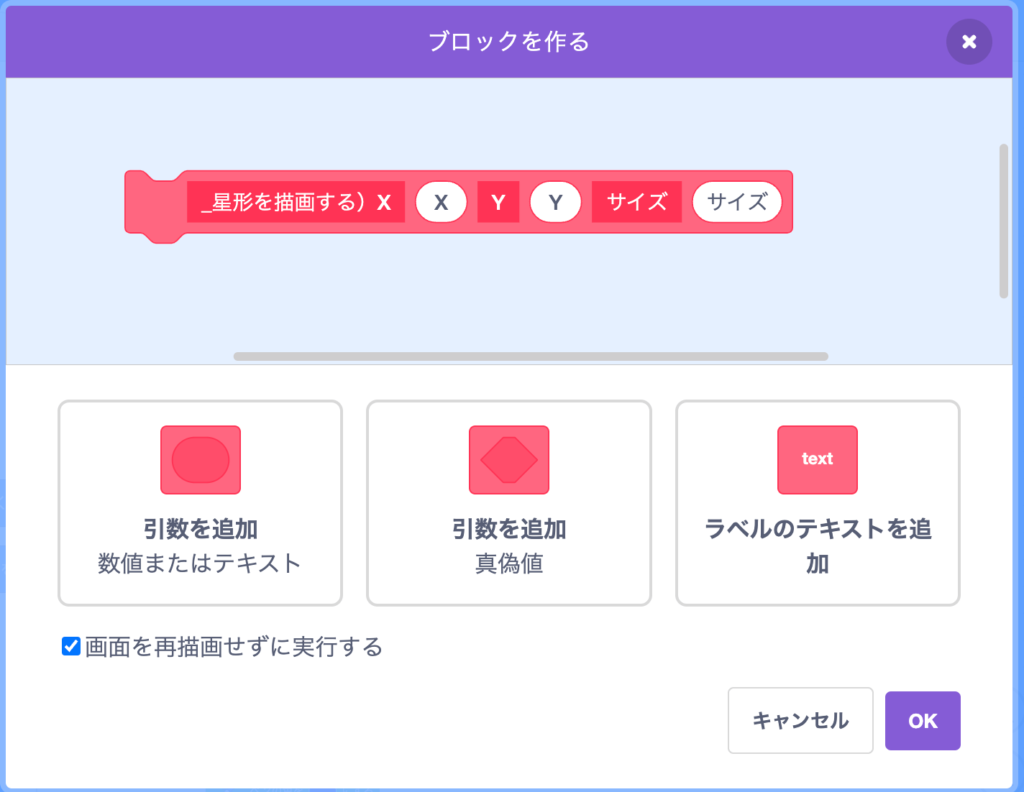
さっき四角形でも作った、ペンを上げて下ろすコーディングを作る。ただし座標にいれる引数は違うぞ。

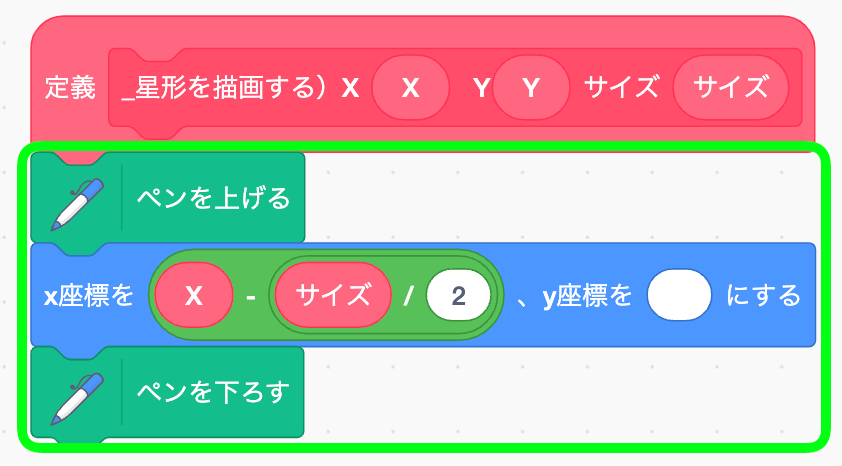
Y座標には複雑な演算をはめていく！心して挑むのだ。

まずスクショの通りに演算ブロックを置いてから、矢印の通りに合体させよう。

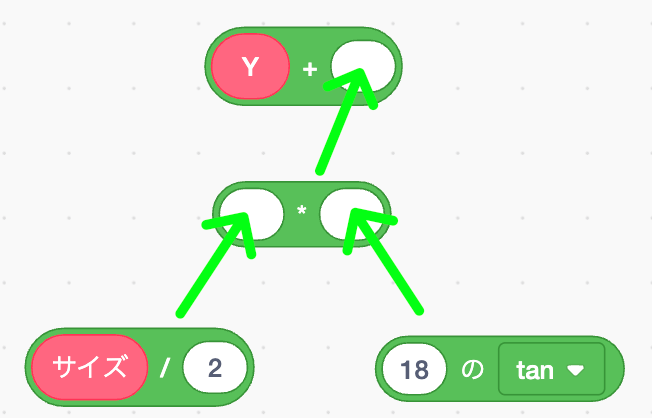
大合体後はこうなる。

• tanってなに？

  tanは、牛タン、、、美味しいよね、じゃなくて！タンジェントと読むのだ。三角関数といって高校で習うんだけど、最近は中学でも理解している人が多いし、なんかスクラッチャーに関しては小学生でも使いこなしてる人増えてきた。ちなみに私はたいして深く理解してない（爆）いや、自分は文系だし？タンジェントは覚えなくていいって高校の時に先生に言われた（国際語学科という数学やらなくていい学科でした）よし、言い訳をちゃんと理解してくれたかな（笑）

tan（タンジェント）とは

超カンタンに説明してみる。坂だ。まず坂を思い浮かべるんだ。どっかにあるでしょ。学校に行く道や駅に行く途中とか。ないなら階段の脇にあるスロープとかでもいい。

例えば坂の長さが5mで高さが1.62mだったとしよう。身長が1.62mくらいの人が身近にいるかもしれないね。そのくらいの高さだ。

で、この坂は1m進むごとに何cmずつ高くなるでしょうみたいな問題ありそうじゃない？

あったらどうする？私なら逃げる（笑）いや、待て。立ち向かうんだ！逃げちゃ駄目だ逃げちゃ駄目だ逃げちゃ駄目だ、、、っ！

ミサトさん「シンジくん、タンジェントを求めるのよ！」

ハッ！いまミサトさんの声が、そうか、タンジェントの説明をしているんだった。

坂の長さと高さを使って「1.62 ÷ 5」っていう計算をしてみる。答えは0.324だ。もちろん暗算した。暗算してない証拠はないからだ。

「この坂は1m進むごとに0.324（つまり32.4cm）ずつ高くなる」というのが解答になる。そしてこの0.324が、この坂のタンジェントだ。

18ってなに？

さっき作ったブロックは「18のtan」だったよね。この18の正体は角度なんだ。星形の小さな三角形の鋭角が18度になるから、ここでは18って数字を使ってる。

でもY座標の値を算出したいから角度のままじゃあ使えない。そこで角度を座標にも使える値（高さ）に変換するために、タンジェントを使っている。

よし、今日のところはこの辺にしておこう（笑）スクラッチに戻るぞ！

Y座標のところにはめてくれ。

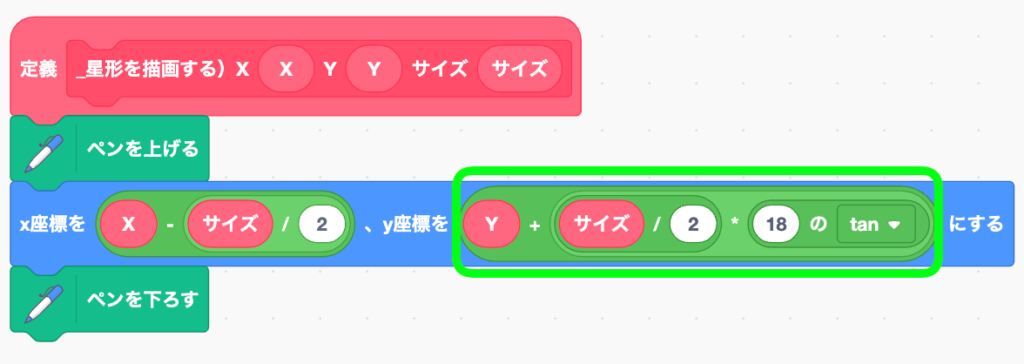
四角形の時と同じように、この下に繰り返しブロックを置いていく。

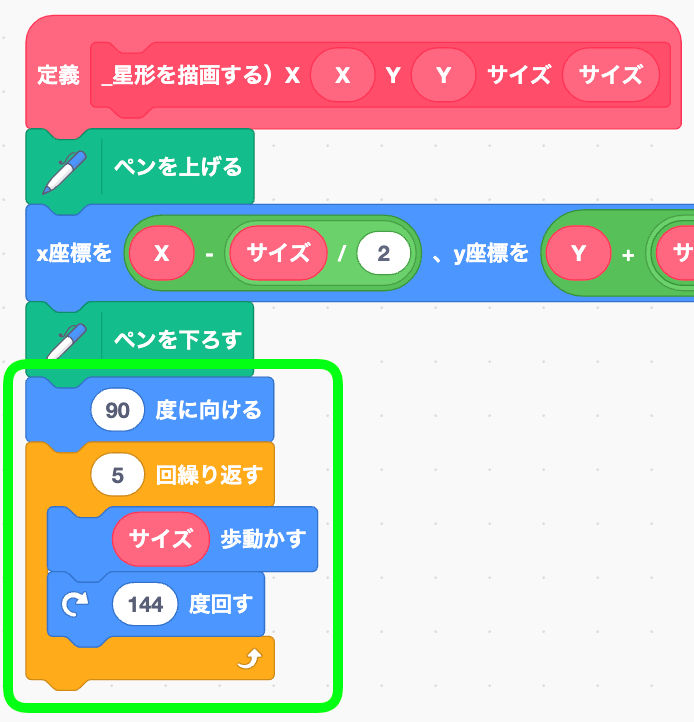
最初にいったん90度に向けているのは、念のため。

図形を描画するところで実行する

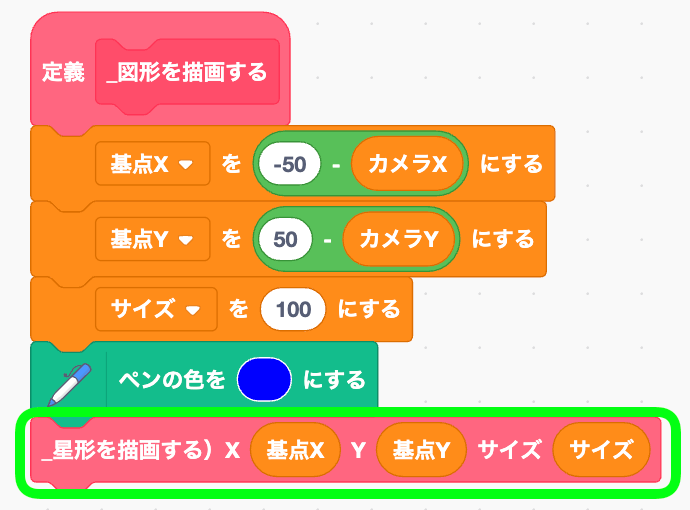
星が描けたかテストする

こんな感じになった？

さらに増やそう。大きさを変えてみるぞ。

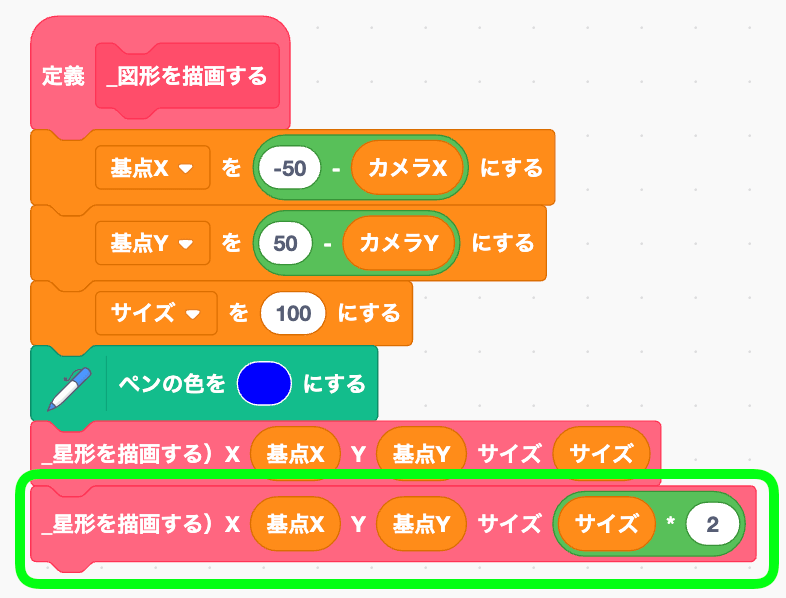
ダブルスター！！

もういっちょ！

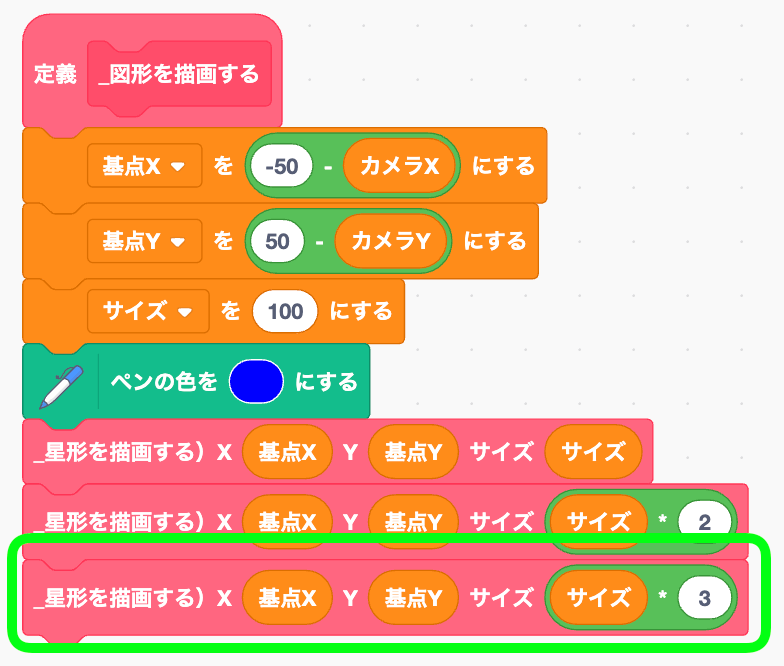
トリプルスター！！！

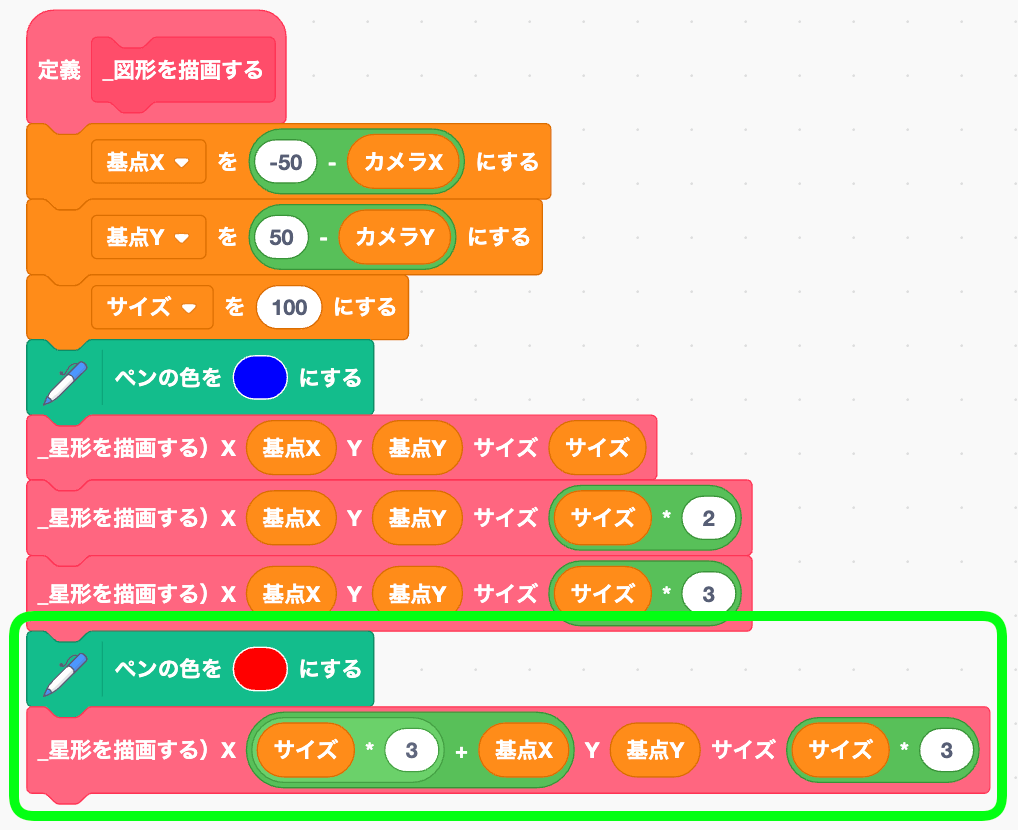
赤い星も隣に描き足してみよう。

まとめ

今回のペン道部の部活動はここまでだ。しかし、常在戦場だ。常にペンを使うチャンスを伺い、脳内の理想をリアルに描画していくんだ（謎）